3.2
Impact Factor
ISSN: 1449-1907
Int J Med Sci 2020; 17(13):2031-2039. doi:10.7150/ijms.46231 This issue Cite
Research Paper
Investigation of Binding Affinity between Potential Antiviral Agents and PB2 Protein of Influenza A: Non-equilibrium Molecular Dynamics Simulation Approach
1. Institute for Computational Science and Technology, Ho Chi Minh City, Vietnam.
2. VNUHCM-University of Technology, Ho Chi Minh City, Vietnam.
Received 2020-3-22; Accepted 2020-7-9; Published 2020-7-25
Abstract
The PB2 protein of the influenza virus RNA polymerase is a major virulence determinant of influenza viruses. It binds to the cap structure at the 5' end of host mRNA to generate short capped RNA fragments that are used as primers for viral transcription named cap-snatching. A large number of the compounds were shown to bind the minimal cap-binding domain of PB2 to inhibit the cap-snatching machinery. However, their binding in the context of an extended form of the PB2 protein has remained elusive. A previous study reported some promising compounds including azaindole and hydroxymethyl azaindole, which were analyzed here to predict binding affinity to PB2 protein using the steered molecular dynamics (SMD) and molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) methods. The results show that the rupture force (Fmax) value of three complexes is in agreement with the binding free energy value (ΔGbind) estimated by the MM-PBSA method, whereas for the non-equilibrium pulling work (Wpull) value a small difference between A_PB2-4 and A_PB2-12 was observed. The binding affinity results indicate the A_PB2-12 complex is more favorable than the A_PB2-4 and A_PB2-16 complexes, which means the inhibitor (12) has the potential to be further developed as anti-influenza agents in the treatment of influenza A.
Keywords: Azaindole (4 and 16), hydroxymethyl azaindole (12), protein_PB2, SMD, MM-PBSA
Introduction
Both seasonal and pandemic influenza have been causing severe illness and death for both humans and farm animals [1]. The virus variants have emerged and posed a constant threat to human health. Changes in viral genes often result in viral evolutionary advantages, such as the degree of virulence and the more efficient replication and transmissibility of the virus [2].
There has been four main influenza A pandemics, including the H1N1 Spanish flu (1918), the H2N2 Asian flu (1957), the H3N2 Hong Kong flu (1968), and the H1N1 swine flu (2009) [3,4]. These have been examples of fast transmission of animal influenza viruses to humans [5]. Although vaccination could prevent influenza for 70-90% of healthy adults [6,7], it is only effective against a limited range of strains and it practically has no effect against new and potentially pandemic strains [8-10]. Therefore, the development of effective drugs against influenza is currently considered as a high priority by different governmental and international agencies, especially by pharmaceutical industries at the worldwide scale.
The influenza virus is an enveloped virus, in which the outer layer is a lipid membrane, which is taken from the host cell where the virus multiplies [11,12]. A glycoprotein is a type of protein molecule linked to sugar. When it is located in a cell membrane, it helps to identify and communicate with the cell. The cell uses the glycoproteins embedded in the plasma membrane to get the oligosaccharides on the outside of the cell, which is typically decorated with different oligosaccharides such as hemagglutinin (HA) [13,14] and neuraminidase (NA) [15]. The NA protein is actually the target of the antiviral drugs Relenza and Tamiflu [16,17]. Additionally, the M2 protein is also a membrane protein and is a target of the antiviral Adamantanes (including Amantadine and Rimantadine) [18,19]. However, the long-term effectiveness of these drugs is a matter of great concern due to the emergence of drug-resistant strains of the virus. Thus, there is an urgent need for new agents to prevent and treat the influenza virus infection, especially in high-risk groups and during pandemic influenza.
Some previous studies showed that some small molecule inhibitors were able to make novel targets in the influenza life cycle against [20-30]. The genome of the influenza virus includes eight different ribonucleoprotein complexes that enclose eight viral genomic RNA segments. Similarly to other negative-stranded RNA viruses, the viral RNA polymerase of influenza virus is always packaged in the infectious virion as a complex with the nucleoprotein [31-34]. The RNA-dependent RNA polymerase of influenza virus is composed of the PA, PB1, and PB2 subunits. A heterotrimeric polymerase is required for RNA transcription and replication that take place in the nucleus during influenza virus infection [33].
The influenza virus is based on a cap-snatching mechanism to accomplish its transcription [35]. Following the entrance of the ribonucleoprotein complexes into the nucleus, the 5' cap of the host pre-mRNA in the nucleus is captured by the cap-binding domain of PB2 [36]. Together with 10-13 nucleotides downstream, the 5' cap is subsequently cleaved off by the N-terminal cap-dependent endonuclease of PA [37]. This 5'-capped oligonucleotide is used as the primer for initiation of the viral transcription by PB1 [38]. This process is called as a “cap-snatching” mechanism, which allows the endonuclease to cleave the 5' caps from host RNAs, and then the latter act as transcription primers [39]. Clearly, the PB2 subunit is linked to the initiation of viral transcription and is known as a cap-binding protein [40-42]. According to recent studies, a cap-primer-dependent in vitro RNA synthesis is affected by the PB2 gene and, therefore, a series of in vitro inhibitors has supported such role for PB2 [43]. monoclonal antibodies specific for the PB2 subunit have interfered with the initiation step of mRNA-primed transcription in vitro [44], and antibodies monospecific for the C terminus of PB2 have inhibited cap snatching and cap-dependent transcription in vitro but not cap-binding [45]. Moreover, antibodies directed to the region from positions 300 to 550 in PB2 inhibited cap snatching and partially affected cap recognition [46,47]. However, the activities of both transcription and cap-dependent endonuclease have required the presence of all three subunits of the polymerase and the RNA template [48, 49].
To elucidate some crucial molecular determinants for the interaction of some inhibitors with PB2 protein of influenza A (protein_PB2), the binding affinity of the azaindole (4&16) and hydroxymethyl azaindole (12) for PB2 protein was predicted. For this purpose, the different theoretical methods including steered molecular dynamics (SMD) [50-52] and Molecular Mechanics Poisson-Boltzmann Surface Area (MM-PBSA) [53,54] were used to compute the binding affinities of these inhibitors for protein_PB2.
Materials and Method
Preparing the structures
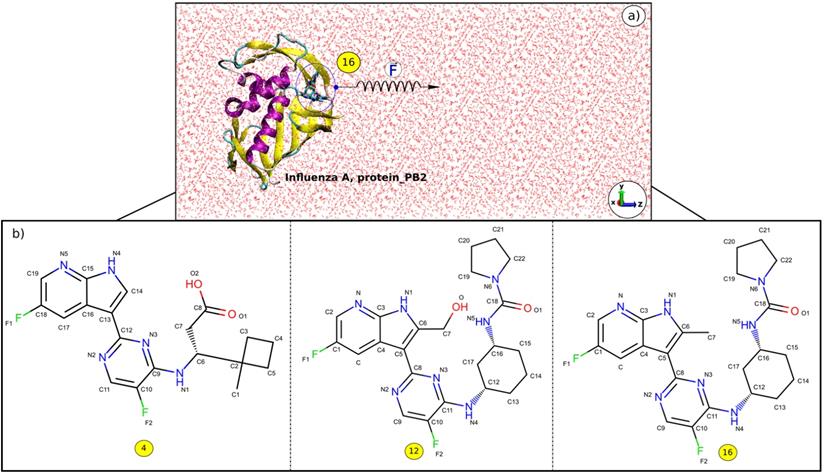
The 3D structures of the complexes were taken from Protein Data Bank with PDB ID: 5JUN (A_PB2-4) [55], 5BUH (A_PB2-12) and 5F79 (A_PB2-16) [56]. The 2D structures of the inhibitors (4), (12) and (16) are shown in Figure 1. The inhibitor topologies and coordinate files were generated by using Swiss Param [57].
Molecular dynamics simulations
Molecular dynamics simulation
The simulation processes of complexes were conducted by using CHARMM 27 force field [58] implemented in the GROMACS 5.1.2 package [58] at absolute temperature 300 K. The TIP3P water model [60] was used in all simulation systems. All distance bonds within the proteins were constrained by the Linear Constraint Solver (LINCS) algorithm [61]. The electrostatic and van der Waals interactions were used to depict non-bonded interactions, with the non-bonded interaction pair-list being updated every 10 fs using a cutoff of 1.4 nm. The Particle Mesh Ewald truncation method [62] was used to treat the long-range electrostatic interactions. From these structures, short 2 ns MD simulations were performed in the NVT ensemble, which were followed by 3 ns NPT simulation. The leap-frog algorithm [63] was used to integrate the equations of motion with the time step set to 2 fs for the MD simulations.
Steered molecular dynamics (SMD) simulation
Choosing a pathway
Caver 3.0 [64] package was used to determine the pulling pathway through the widest tunnel as this minimizes the occurrence of collisions between the inhibitor and protein_PB2 during the simulation. Then the Caver 3.0 and PyMOL [65] packages were employed to rotate the protein_PB2 in such a way that the inhibitor unbinding pathway is along the z-axis (Figure 1).
Preparing Steered Molecular Dynamics (SMD) simulation
In the Steered Molecular Dynamics (SMD) simulation [50-52], each of the inhibitor-protein_PB2 complexes was placed in a triclinic box of 6nm × 6nm × 14 nm to have enough space to pull the inhibitor out of the binding site. The three-dimensional coordinates of the center of the complex were 3nm × 3nm × 3 nm. The complexes were immersed in a salt solution with a concentration of 0.15 M of sodium and chloride to neutralize the total charge.
The pulling force is measured according to the following equation:
(1)
where 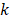 is the force constant,
is the force constant, 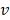 is the pulling velocity,
is the pulling velocity, 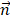 is the pulling direction normal,
is the pulling direction normal, 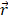 and
and 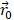 are the positions of protein at time
are the positions of protein at time 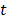 and initial time, respectively. During the simulations, the spring constant
and initial time, respectively. During the simulations, the spring constant 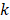 value was set to 600 kJ/ (mol.nm2) (approximately 1020 pN/nm), which is a typical value used in atomic force microscope (AFM) experiments [66]. The complete dissociation of the inhibitor from the binding pocket of protein_PB2 was reached during 500 ps for three complexes with pulling velocity set at
value was set to 600 kJ/ (mol.nm2) (approximately 1020 pN/nm), which is a typical value used in atomic force microscope (AFM) experiments [66]. The complete dissociation of the inhibitor from the binding pocket of protein_PB2 was reached during 500 ps for three complexes with pulling velocity set at 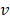 = 0.005 nm/ps.
= 0.005 nm/ps.
In order to calculate the relative binding affinities of the complexes using the SMD simulation, the non-equilibrium pulling work profile was used to evaluate a scoring function to rank the binding affinities between the inhibitor and protein. The non-equilibrium pulling work 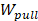 is approximately defined as follows:
is approximately defined as follows:
(2)
where 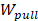 is the non-equilibrium pulling work of external force
is the non-equilibrium pulling work of external force 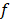 , and
, and 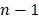 is the number of steps in the SMD simulation,
is the number of steps in the SMD simulation, 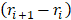 is the inhibitor displacement in step i, here the centers of mass (COM) of the inhibitors were employed to measure the inhibitor displacement.
is the inhibitor displacement in step i, here the centers of mass (COM) of the inhibitors were employed to measure the inhibitor displacement.
MM-PBSA free energy calculations
To estimate binding free energy between the inhibitors and protein_PB2, each snapshot extracted from the equilibrium MD simulation was used to estimate the binding free energy using the MM-PBSA method. The binding free energy of the inhibitor-protein is computed by this approach as follows [53,54]:
(3)
where 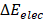 and
and 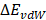 are contributions of electrostatic and vdW energies, respectively [67].
are contributions of electrostatic and vdW energies, respectively [67]. 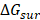 and
and 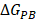 are non-polar and polar solvation energies [68]. Here,
are non-polar and polar solvation energies [68]. Here, 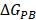 derived from the electrostatic potential between solute and solvent was determined using the continuum solvent approximation [69]. It is the change of electrostatic energy from transferring solute in a continuum medium, from a low solute dielectric constant (ε = 2) to a higher one with water without salt (ε = 78.45). Using a grid spacing of 0.1 Å, the APBS package [70] was implemented for numerical solution of the corresponding linear Poisson-Boltzmann equation. The nonpolar solvation term
derived from the electrostatic potential between solute and solvent was determined using the continuum solvent approximation [69]. It is the change of electrostatic energy from transferring solute in a continuum medium, from a low solute dielectric constant (ε = 2) to a higher one with water without salt (ε = 78.45). Using a grid spacing of 0.1 Å, the APBS package [70] was implemented for numerical solution of the corresponding linear Poisson-Boltzmann equation. The nonpolar solvation term 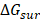 was approximated as linearly dependent on the solvent accessible surface area (SASA), derived from Shrake-Rupley numerical method [71] integrated in the APBS package.
was approximated as linearly dependent on the solvent accessible surface area (SASA), derived from Shrake-Rupley numerical method [71] integrated in the APBS package. 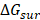 = γSASA + β, where γ = 0.0072 kcal/mol.Å2 and β = 0 [72]. The entropic contribution
= γSASA + β, where γ = 0.0072 kcal/mol.Å2 and β = 0 [72]. The entropic contribution 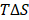 is determined using the normal mode approximation [73].
is determined using the normal mode approximation [73].
Measures used in data analysis
The contact networks between the inhibitors and protein_PB2 were determined by using the LigPlot and PyMOL packages [65,74]. The root mean square deviation (RMSD), the number of hydrogen bond (H-bond) and the number of contacts (NC) were calculated by the “gmx_mpi hbond” and “gmx_mpi mindist” tools in the GROMACS package. The standard errors of the mean (E) are approximately estimated as follows:
(4)
Where N is the number of snapshots, xi is a quantity at each snapshot, and 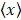 is the average value of xi.
is the average value of xi.
Results
The contact network and stability of the complexes
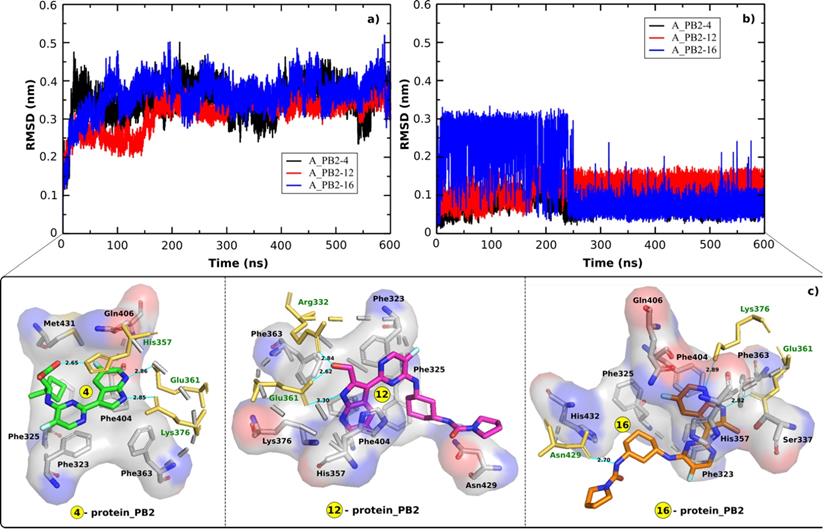
In order to indicate the stability of the systems including A_PB2-4, A_PB2-12, and A_PB2-16, the RMSD time profiles calculated for protein_PB2's backbone and the inhibitor's heavy atoms are shown in Figure 2A & B for every analyzed system. The RMSD values reveal that the three systems reached equilibrium after 250 ns when the RMSD values start fluctuating around about 0.3 nm and 0.45 nm for the backbone of protein_PB2 and around 0.1 nm for the inhibitor's heavy atoms in all cases. The snapshots collected from the last 100 ns of MD simulations were used to calculate the binding free energy through the MM-PBSA method.
a) z-direction of the inhibitor (16) exiting the binding pocket of protein_PB2, and b) 2D structures of the inhibitors (4), (12), and (16).
RMSD time profiles for a) the backbone of protein_PB2 in the three complexes and b) the heavy atoms of three inhibitors. c) the contact network between three inhibitors and protein_PB2. Residues shown in yellow form H-bonds (cyan lines) with the ligands.
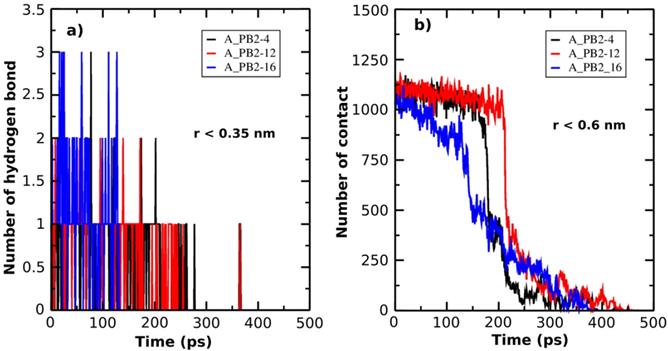
The number of H-bonds (a) and the number of NC (b) formed between protein_PB2 and the inhibitors are presented as a function of SMD simulation time.
The contact network has an important role in stabilizing energetically favored inhibitors. Figure 2C displays the contact network between three inhibitors and protein_PB2. By analyzing the interfaces we found the following interactions:
- Both Glu361 and Lys376 form H-bonds with the inhibitors (4) and (16), while only Glu361 forms a H-bond with the inhibitor (12). The Glu361 residue seems to drive the interactions of the inhibitors-protein_PB2 systems. There are three residues forming H-bonds with the inhibitor (4) (Glu361, Lys376, and His357) and the inhibitor (16) (Glu361, Lys376, and Asn429), while only two residues (Glu361 and Arg332) establish H-bonds with the inhibitor (12).
- Most of the H-bonds formed at the interfaces of the three complexes involve side chains of charged (Arg332, His357, Glu361, Lys376) residues, with Asn429 being the only neutral residue whose side chain forms H-bonds with one of the compounds (16). The polar interaction energy can make a large contribution in estimating the binding affinity between the inhibitors and protein_PB2.
The H-bond between the inhibitors and protein_PB2 has an important role in the binding affinity of the complexes. Therefore, the average H-bond occupancies (during the last 100 ns of the MD simulations) were also calculated to determine the contribution of each residue at the interfaces in each complex. The results indicate that the Phe323, Phe325, His357, Glu361, Phe363, Lys376, and Phe404 residues are involved in the formation of a H-bond network in the three complexes (Table 1). Most of the residues forming the contact network with three inhibitors are the Phe aromatic residues. That means the Phe residues can have a key role in interactions with the inhibitors and lead to the change of the binding affinity of the inhibitors for protein_PB2.
Average occupancies of H-bonds between the inhibitors and protein_PB2 in the three A_PB2-4, A_PB2-12, and A_PB2-16 complexes, determined from the last 100 ns of the MD simulations
| Residue | Inhibitor (4) | Inhibitor (12) | Inhibitor (16) |
|---|---|---|---|
| Phe323 (O) | 0.1873 (N4) | 0.0055 (N1) | 0.0044 (F2) |
| Phe325 (O) | 0.0431 (N4) | 0.1101 (F2) | 0.0112 (N5) |
| Arg332 (N) | 0.4688 (N2, F1, O) | ||
| Ser337 (O) | 0.0019 (N) | ||
| His357 (N) | 0.6012 (O1, O2) | 0.2155 (N2, O, F1, F2) | 0.0377 (O1, F2) |
| Glu361 (O) | 0.5202 (N5) | 0.8033 (N1, O) | 0.5010 (N1) |
| Phe363(O) | 0.0323(N4) | 0.0795 (N1) | 0.2188 (N1) |
| Lys376 (N) | 0.4432 (N4) | 0.1113 (N, O) | 0.6212 (N) |
| Phe404 (O) | 0.2261 (F1) | 0.2278 (O) | 0.0220 (N) |
| Gln406 (N) | 0.0110 (N5) | 0.0060 (N, N2, F1, F2) | |
| Asn429 (N) | 0.2032 (N6, O1, F1) | 0.5721 (F1, N5) | |
| Met431 (O) | 0.0032 (N4) | ||
| His432 (N) | 0.0731 (O1) |
Additionally, in order to describe the unbinding process of the inhibitor-protein_PB2 complexes, the H-bond (r < 0.35nm) and the NC (r < 0.6nm) are determined as a function of simulation time (Figure 3A & B). At the bound state, there are three H-bonds formed between inhibitors (4) and (16) and protein_PB2, while there are only 2 H-bonds between inhibitor (12) and protein_PB2. At the unbound state, the number of H-bonds decreases to 0 for all three complexes. Likewise, the NC value also helps follow the unbinding process of the inhibitor-protein_PB2 complexes. There are roughly 1125 NCs formed between the three inhibitors and protein_PB2 at the bound state, which decrease to 0 NCs after 400 ps for inhibitor (4), after 425 ps for inhibitor (16) and after 450 ps for inhibitor (12) at the unbound state. Although the NC and the number of H-bonds of the A_PB2-16 complex are greater than those of the A_PB2-4 and A_PB2-12 complexes, the NC and the number of H-bonds of the A_PB2-16 complex reach 0 faster than those of the A_PB2-4 and A_PB2-12 complexes.
Binding affinity between the inhibitors and protein_PB2
Binding affinity is widely used to evaluate and rank order strength of biomolecular interactions in biological systems. In this research, to make a full understanding of the binding mechanism of these inhibitors to protein_PB2, we estimated the binding affinity of the azaindole (4&16) and hydroxymethyl azaindole (12) to protein_PB2.
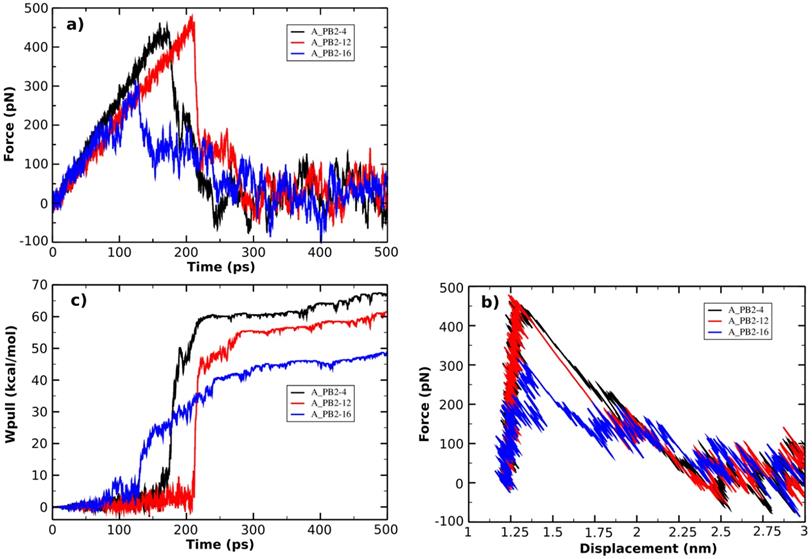
The SMD is used as a method to study the unbinding process of small molecules (the inhibitors) from a large molecule (protein_PB2) and is capable of rank the compounds binding a same target protein according to their relative binding affinities [75]. The pulling force profile is started as a function of time (shown in Figure 4A). The Fmax has an important role to indicate the dissociation between protein_PB2 and the inhibitors. Here the pulling force profile is able to show the division of two consecutive stages: During the first stage, the pulling force continuously increased until the inhibitors started to dissociate from protein_PB2, and the external force reached the Fmax value when the H-bonds are broken. During the second stage, the pulling force started to decrease as the inhibitors are exiting the binding pocket of protein_PB2. In more detail, the largest pulling force of the A_PB2-12 complex (Fmax = 477.50 pN, t=220 ps) is larger than those of the A_PB2-4 complex (Fmax = 462.42 pN, t=170 ps) and the A_PB2-16 complex (Fmax = 315.86 pN, t=125 ps), respectively. Overall, the variation of pulling force profiles among the inhibitor-protein_PB2 complexes could be attributed to the binding site of protein_PB2. Moreover, the evolution of the steering force during the inhibitor displacement first showed a linear behavior which then became nonlinear before the Fmax value was reached (seen from Figure 4B). At this point, the inhibitor is still located in the binding pocket. After obtaining the Fmax value, the force value decreased steeply and fluctuated around zero value (beginning at 2.25 nm), when the inhibitor detached from the protein_PB2 along the pulling direction.
(a) Force vs time and (b) force vs displacement profiles. (c) Pulling work-time profile.
Binding affinity values of three inhibitors for protein_PB2, estimated from the MM-PBSA method and SMD simulations
| ΔEelec (kcal/mol) | ΔEvdW (kcal/mol) | ΔGsur (kcal/mol) | ΔGPB (kcal/mol) | -TΔS (kcal/mol) | ΔGbind (kcal/mol) | Fmax (pN) | Wpull (kcal/mol) | |
|---|---|---|---|---|---|---|---|---|
| (4) | -7.63±1.77 | -2.17±0.25 | -6.95±1.05 | 6.19±1.31 | 0.52±0.02 | -10.04±1.63 | 462.42±47.12 | 77.13±8.25 |
| (12) | -16.43±3.15 | -3.60±0.11 | -6.77±2.02 | 6.74±1.73 | 7.36±1.24 | -12.70±1.41 | 477.50±51.61 | 72.04±7.77 |
| (16) | -7.71±1.14 | -1.86±0.05 | -4.41±0.93 | 7.05±1.79 | 0.49±0.02 | -6.44±1.12 | 315.86±39.32 | 55.12±6.75 |
The non-equilibrium pulling work (Wpull) is also used to predict the relative binding affinity of protein_PB2-inhibitor systems (eq. 2). As seen from Figure 4C, the Wpull rapidly increased as the pulling force does, until the inhibitors come out from the binding pocket of protein_PB2. It reached a stable value when the inhibitors lost their non-bonded contacts with protein_PB2 (corresponding to 50 kcal/mol for (16), 60 kcal/mol for (12) and 65 kcal/mol for (4)). However, note that small fluctuations occur, which can be neglected. All three systems reach a stable state after 250 ps.
In this work, the MM-PBSA method is also used to estimate the binding free energies and makes possible to indicate the contribution of each energy component to the inhibitor's potency. As seen in Table 2, the contribution of different energy components to the ΔGbind indicates that the electrostatic energy (ΔEelec) has a more important role than the vdW energy (ΔEvdW). The changes in the nonpolar solvation energy (ΔGsur) values significantly contributed to the difference of the ΔGbind among the complexes. The entropy (-TΔS) of the A_PB2-12 complex is larger than those of the A_PB2-4 and A_PB2-16 complexes. The loss of polar solvation energy (ΔGPB) is compensated by the remaining components of the ΔGbind in these systems.
Specifically, the ΔEelec obtained from the complex formation compensates the loss in ΔGPB. Here, the ΔEelec of the A_PB2-12 complex (-16.43 kcal/mol) is more negative than those of both remaining complexes (-7.63 kcal/mol for the A_PB2-4 complex, and -7.71 kcal/mol for the A_PB2-16 complex). The ΔGvdW values of the three complexes (ranged from -1.86 to -3.60 kcal/mol) do not lead to the difference of their ΔGbind values. Conversely, the ΔGsur values of these complexes significantly contribute to the difference of their ΔGbind values (ranged from -6.95 to -4.41 kcal/mol). The entropy contribution (-TΔS) of the A_PB2-12 complex (7.36 kcal/mol) is greater than those of the A_PB2-4 and A_PB2-16 complexes (0.52 kcal/mol for the A_PB2-4 complex, and 0.49 kcal/mol for the A_PB2-16 complex). Clearly, the OH group of inhibitor (12) is not only yielded to a more negative value of electrostatic energy but also contributed to making a fairly large entropic energy. Here, the -TΔS value of the A_PB2-12 complex contributed appreciably to the change of the binding free energy while this energy component has a negligible impact on the binding free energy to two remaining complexes. Finally, the ΔGbind of the A_PB2-12 complex (-12.70 kcal/mol) is lower than that of both remaining complexes (-10.04 kcal/mol for the A_PB2-4 complex, and -6.44 kcal/mol for the A_PB2-16 complex). The results indicate that the affinity of inhibitor (12) bound for protein_PB2 is stronger than that of inhibitors (4) and (16). Moreover, our calculations reveal that the Fmax of three complexes is in good agreement with the ΔGbind value, while the Wpull value has a small difference between A_PB2-4 and A_PB2-12. In short, the inhibitor (12) has the potential to be further developed as anti-influenza agents in the treatment of influenza A.
Concluding Remarks
In the present theoretical study, we applied the SMD and MM-PBSA methods to predict the binding affinity of three inhibitors for protein_PB2. A number of interesting results emerged from our work, which can be summarized as follows:
- The results from the MM-PBSA method showed that the electrostatics (ΔEelec) interaction plays a more important role than the van der Waals (ΔEvdW) component in contributing to the binding free energy value of all three complexes. Additionally, the entropy (-TΔS) of the A_PB2-12 complex has a large detrimental impact on the binding free energy while it makes no significant contribution to the binding free energies of the A_PB2-4 and A_PB2-16 complexes.
- The Fmax value of three complexes is in agreement with the ΔGbind value, while the Wpull value a small difference between the A_PB2-4 and A_PB2-12 complexes was observed. The binding affinities showed that the affinity of inhibitor (12) for protein_PB2 is stronger than that of inhibitors (4) and (16).
Supplementary Material
Supplementary parameterization scheme.
Acknowledgements
We sincerely thank Prof. Mai Suan Li from the Institute of Physics, Polish Academy of Science, Poland; for supporting and valuable comments. This research was funded by the Department of Science and Technology - Ho Chi Minh City (HCMC - DOST), and the Institute for Computational Science and Technology (ICST) at Ho Chi Minh City, Vietnam under Contract No.14/2018/HĐ-KHCNTT. The computing resources were provided by the Institute for Computational Science and Technology at Ho Chi Minh City, Vietnam.
Author Contributions
HN conceived the experiment. TP and HN conducted the experiment. TP, HLN, TP-T and HN analyzed the results. HN wrote the paper. All authors reviewed the manuscript.
Competing Interests
The authors have declared that no competing interest exists.
References
1. Imai M, Watanabe T, Hatta M, Das SC, Ozawa M, Shinya K, Zhong G, Hanson A, Katsura H, Watanabe S, Li C, Kawakami E, Yamada S, Kiso M, Suzuki Y, Maher EA, Neumann G, Kawaoka Y. Experimental adaptation of an influenza H5 HA confers respiratory droplet transmission to a reassortant H5 HA/H1N1 virus in ferrets. Nature. 2012;486:420-428
2. Herfst S, Schrauwen EJ, Linster M, Chutinimitkul S, de Wit E, Munster VJ, Sorrell EM, Bestebroer TM, Burke DF, Smith DJ, Rimmelzwaan GF, Osterhaus AD, Fouchier RA. Airborne transmission of influenza A/H5N1 virus between ferrets. Science. 2012;336:1534-1541
3. Taubenberger JK, Reid AH, Krafft AE, Bijwaard KE, Fanning TG. Initial genetic characterization of the 1918 ''Spanish” influenza virus. Science. 1997;275:1793-1796
4. Garten RJ, Davis CT, Russell CA, Shu B, Lindstrom S, Balish A, Sessions WM, Xu X, Skepner E, Deyde V, Okomo-Adhiambo M, Gubareva L, Barnes J, Smith CB, Emery SL, Hillman MJ, Rivailler P, Smagala J, de Graaf M, Burke DF, Fouchier RA, Pappas C, Alpuche-Aranda CM, López-Gatell H, Olivera H, López I, Myers CA, Faix D, PJ Blair, Yu C, Keene KM, Dotson Jr PD, Boxrud D, Sambol AR, Abid SH, St George K, Bannerman T, Moore AL, Stringer DJ, Blevins P, Demmler-Harrison GJ, Ginsberg M, Kriner P, Waterman S, Smole S, Guevara HF, Belongia EA, Clark PA, Beatrice ST, Donis R, Katz J, Finelli L, Bridges CB, Shaw M, Jernigan DB, Uyeki TM, Smith DJ, Klimov AI, Cox NJ. Antigenic and genetic characteristics of swineorigin, A (H1N1) influenza viruses circulating in humans. Science. 2009;325:197-201
5. Mehle A, Doudna JA. Adaptive strategies of the influenza virus polymerase for replication in humans. Proc Natl Acad Sci U S A. 2009;106:21312-21316
6. Demicheli V, Rivetti D, Deeks JJ, Jefferson TO. Vaccines for preventing influenza in healthy adults. Cochrane Database Syst Rev. 2004: 7:CD001269.
7. Patriarca PA, Weber JA, Meissner MK, Stricof RL, Dateno B, Braun JE, Arden NH, Kendal AP. Use of influenza vaccine in nursing homes. J Am Geriatr Soc. 1985;33:463-466
8. Nichol KL, Wuorenma J, von Sternberg T. Benefits of influenza vaccination for low-, intermediate-, and high-risk senior citizens. Arch Intern Med. 1998;158:1769-1779
9. Glezen WP, Decker M, Perrotta DM. Survey of underlying conditions of persons hospitalized with acute respiratory disease during influenza epidemics in Houston, 1978-1981. Am Rev Respir Dis. 1987;136:550-555
10. Baughman BM, Jake Slavish P, DuBois RM, Boyd VA, White SW, Webb TR. Identification of influenza endonuclease inhibitors using a novel fluorescence polarization assay. ACS Chem Biol. 2012;7:526-534
11. Judith MF, Nicolle M, Hui T, John S, Anice CL. Influenza virus reassortment is enhanced by semi-infectious particle but can be suppresses by defective interfering particles. PLoS Pathog. 2015;11:e1005204
12. Christopher BB. Biological activities of “noninfectious” influenza A virus particles. Future Virol. 2014;9:41-51
13. Wiley D, Skehel J. The structure and function of the Hemagglutinin membrane glycoprotein of influenza virus. Annu Rev Biochem. 1987;56:365-394
14. Skehel J, Wiley D. Receptor binding and membrane fusion in virus entry: The Influenza Hemagglutinin. Annu Rev Biochem. 2000;69:531-569
15. Colman P, Varghese J, Laver W. Structure of the catalytic and antigenic sites in influenza virus neuraminidase. Nature. 1983;303:41-44
16. Smith BJ, McKimm-Breshkin JL, McDonald M, Fernley RT, Varghese JN, Colman PM. Structural studies of the resistance of influenza virus neuraminidase to inhibitors. J Med Chem. 2002;45:2207-2212
17. Nguyen H, Tran T, Fukunishi Y, Higo J, Nakamura H, Le L. Computational study of drug binding affinity to influenza A Neuraminidase using smooth reaction path generation (SRPG) method. J Chem Inf Model. 2015;55:1936-1943
18. Nguyen H, Le L. Steered molecular dynamics approach for promising drugs for influenza A virus targeting M2 channel proteins. Eur Biophys J. 2015 44(6), 447-455
19. Nguyen HV, Nguyen HT, Le LT. Investigation of the free energy profiles of Amantadine and Rimantadine in the AM2 binding pocket. Eur Biophys J. 2016;45:63-70
20. Hayden F. Developing new antiviral agents for influenza treatment: what does the future hold? Clin Infect Dis. 2009;48(Suppl 1):S3-S13
21. De Clercq E, Field HJ. Antiviral Chemistry & Chemotherapy's current antiviral agents FactFile (2nd edition): RNA viruses. Antivir Chem and Chemother. 2008;19:63-74
22. Lüscher-Mattli M. Influenza chemotherapy: A review of the present state of art and of new drugs in development. Arch Virol. 2000;145:2233-2248
23. Moscona A. Medical management of influenza infection. Annu Rev Med. 2008;59:397-413
24. Wilson JC, von Itzstein M. Recent strategies in the search for new anti-influenza therapies. Curr Drug Targets. 2003;4:389-408
25. Beigel J, Bray M. Current and future antiviral therapy of severe seasonal and avian influenza. Antiviral Res. 2008;78:91-102
26. Leyssen P, De Clercq E, Neyts J. Molecular strategies to inhibit the replication of RNA viruses. Antiviral Res. 2008;78:9-25
27. Boltz DA, Aldridge JR Jr, Webster RG, Govorkova EA. Drugs in development for influenza. Drugs. 2010;70:1349-1362
28. Das K, Aramini JM, Ma LC, Krug RM, Arnold E. Structures of influenza A proteins and insights into antiviral drug targets. Nat Struct Mol Biol. 2010;17:530-538
29. Hooker L, Strong R, Adams R, Handa B, Merrett JH, Martin JA, Klumpp K. A sensitive, single-tube assay to measure the enzymatic activities of influenza RNA polymerase and other poly(A) polymerases: application to kinetic and inhibitor analysis. Nucleic Acids Res. 2001;29:2691-2698
30. Honda A, Ueda K, Nagata K, Ishihama A. Identification of the RNA polymerase-binding site on genome RNA of influenza virus. J Biochem. 1987;102:1241-1249
31. Noda T, Sagara H, Yen A, Takada A, Kida H, Cheng RH, Kawaoka Y. Architecture of ribonucleoprotein complexes in influenza A virus particles. Nature. 2006;439:490-492
32. Coloma R, Valpuesta JM, Arranz R, Carrascosa JR, Ortín J, Martín-Benito J. The structure of a biologically active influenza virus ribonucleoprotein complex. PLoS Pathog. 2009;5:e1000491
33. Ng AK, Zhang H, Tan K, Li Z, Liu JH, Chan PK, L SM, Chan WY, Au SW, Joachimiak A, Walz T, Wang JH, Shaw PC. Structure of the influenza virus A H5N1 nucleoprotein: implications for RNA binding, oligomerization, and vaccine design. FASEB J. 2008;22:3638-3647
34. Ye Q, Krug RM, Tao YJ. The mechanism by which influenza A virus nucleoprotein forms oligomers and binds RNA. Nature. 2006;444:1078-1082
35. Plotch SJ, Bouloy M, Ulmanen I, Krug RM. A unique cap (m7GpppXm)-dependent influenza virion endonuclease cleaves capped RNAs to generate the primers that initiate viral RNA transcription. Cell. 1981;23:847-858
36. Dias A, Bouvier D, Crépin T, McCarthy AA, Hart DJ, Baudin F, Cusack S, Ruigrok RW. The cap-natching endonuclease of influenza virus polymerase resides in the PA subunit. Nature. 2009;458:914-918
37. Yuan P, Bartlam M, Lou Z, Chen S, Zhou J, He X, Lv Z, Ge R, Li X, Deng T, Fodor E, Rao Z, Liu Y. Crystal structure of an avian influenza polymerase PA(N) reveals an endonuclease active site. Nature. 2009;458:909-913
38. Guilligay D, Tarendeau F, Resa-Infante P, Coloma R, Crepin T, Sehr P, Lewis J, Ruigrok RW, Ortin J, Hart DJ, Cusack S. The structural basis for cap binding by influenza virus polymerase subunit PB2. Nat Struct Mol Biol. 2008;15:500-506
39. Datta K, Wolkerstorfer A, Szolar OH, Cusack S, Klumpp K. Characterization of PA-N terminal domain of Influenza A polymerase reveals sequence specific RNA cleavage. Nucleic Acids Res. 2013;41:8289-8299
40. Blaas D, Patzelt E, Keuchler E. Identification of the cap binding protein of influenza virus. Nucleic Acids Res. 1982;10:4803-4812
41. Shi L, Galarza JM, Summers DF. Recombinant-baculovirus-expressed PB2 subunit of the influenza A virus RNA polymerase binds cap groups as an isolated subunit. Virus Res. 1996;42:1-9
42. Ulmanen I, Broni BA, Krug RM. Role of two of the influenza virus core P proteins in recognizing cap 1 structures (m7GpppNm) on RNAs and in initiating viral RNA transcription. Proc Natl Acad Sci U S A. 1981;78:7355-7359
43. Perales B, de la Luna S, Palacios I, Ortín J. Mutational analysis identifies functional domains in the influenza A virus PB2 polymerase subunit. J Virol. 1996 70(3), 1678-1686
44. Ba´rcena J, Ochoa M, de la Luna S, Melero JA, Nieto A, Ortín J, Portela A. Monoclonal antibodies against influenza virus PB2 and NP polypeptides interfere with the initiation step of viral mRNA synthesis in vitro. J Virol. 1994;68:6900-6909
45. Blok V, Cianci C, Tibbles KW, Inglis SC, Krystal M, Digard P. Inhibition of the influenza virus RNA-dependent RNA polymerase by antisera directed against the carboxy-terminal region of the PB2 subunit. J Gen Virol. 1996;77:1025-1033
46. Masunaga K, Mizumoto K, Kato H, Ishihama A, Toyoda T. Molecular mapping of influenza virus RNA polymerase by site-specific antibodies. Virology. 1999;256:130-141
47. Li ML, Rao P, Krug RM. The active sites of the influenza cap-dependent endonuclease are on different polymerase subunits. EMBO J. 2001;20:2078-2086
48. Cianci C, Tiley L, Krystal M. Differential activation of the influenza virus polymerase via template RNA binding. J Virol. 1995;69:3995-3999
49. Hagen M, Chung TD, Butcher JA, Krystal M. Recombinant influenza virus polymerase: requirement of both 5' and 3' viral ends for endonuclease activity. J Virol. 1994;68:1509-1515
50. Nguyen H, Pham T, Nguyen HL, Phan T. Investigation of binding affinity between Prokaryotic protein (AHU-IHF) and DNAs: Steered molecular dynamics approach. Appl Biochem Biotechnol. 2018;186:834-846
51. Truong DT, Li MS. Probing the binding affinity by Jarzynski's non-equilibrium binding free energy and rupture time. J Phys Chem B. 2018;122:4693-4699
52. Nguyen H, Do N, Phan T, Pham T. Steered molecular dynamics for investigating the interaction between insulin receptor tyrosine kinase (IRK) and variants of protein tyrosine phosphatase 1B(PTP1B). Appl Biochem Biotechnol. 2018;184:401-413
53. Nguyen H, Nguyen T, Le L. Computational study of Glucose-6-phosphate-dehydrogennase deficiencies using molecular dynamics simulation. S Asian J Life Sci. 2016;4:32-39
54. Wang J, Morin P, Wang W, Kollman PA. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J Am Chem Soc. 2001;123:5221-5230
55. Farmer LJ, Clark MP, Boyd MJ, Perola E, Jones SM, Tsai A, Jacobs MD, Bandarage UK, Ledeboer MW, Wang T, Deng H, Ledford B, Gu W, Duffy JP, Bethiel RS, Shannon D, Byrn RA, Leeman JR, Rijnbrand R, Bennett HB, O'Brien C, Memmott C, Nti-Addae K, Bennani YL, Charifson PS. Discovery of novel, orally bioavailable β-Amino acid azaindole inhibitors of influenza PB2. ACS Medical Chemistry Letters. 2017;8:256-260
56. Bandarage UK, Clark MP, Perola E, Gao H, Jacobs MD, Tsai A, Gillespie J, Kennedy JM, Maltais F, Ledeboer MW, Davies I, Gu W, Byrn RA, Nti Addae K, Bennett H, Leeman JR, Jones SM, O'Brien C, Memmott C, Bennani Y, Charifson PS. Novel 2-Substituted 7-Azaindole and 7-Azaindazole Analogues as potential antiviral agents for the treatment of influenza. ACS Med Chem Lett. 2017;8:261-265
57. Zoete V, Cuendet MA, Grosdidier A, Michielin O. SwissParam, a fast force field generation tool for small organic molecules. J Comput Chem. 2011;32:2359-2368 DOI: 10.1002/jcc.21816
58. Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes P, Vorobyov I, MacKerell Jr AD. CHARMM General Force Field (CGenFF): A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J Comput Chem. 2010;31:671-690
59. Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput. 2008;4:435-447
60. Mark P, Nilsson L. Structure and dynamics of the TIP3P, SPC, and SPC/E water models at 298 K. J Phys Chem A. 2001;105:9954-9960
61. Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. LINCS: A linear constraint solver for molecular simulations. J Comput Chem. 1997;18:1463-1472
62. Darden T, York D, Pedersen L. Particle Mesh Ewald: An N log(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089-10092
63. Hockney RW, Goel SP, Eastwood J. Quit high resolution computer models of plasma. J Comput Phys. 1974;14:148-158
64. Petrek M, Otyepka M, Banas P, Kosinova P, Koca1 J, Damborsky J. CAVER: A new tool to explore routes from protein clefts, pockets and cavities. BMC Bioinformatics. 2006;7:316
65. PyMOL: The PyMOL Molecular Graphics System, version 1.3; Schrӧdinger, LLC: Cambridge, MA, 2010
66. Gibson CT, Carnally S, Roberts CJ. Attachment of carbon nanotubes to atomic force microscope probes. Ultramicroscopy. 2007;107:1118-1122
67. Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc Natl Acad Sci U S A. 2001;98:10037-10041
68. Binnig G, Quate CF, Gerber Ch. Atomic force microscope. Phys Rev Lett. 1986;56:930
69. Sharp KA, Honig B. Electrostatic interactions in macromolecules: theory and applications. Annu Rev Biophys Bio. 1990;19:301-332
70. Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc Natl Acad Sci USA. 2001;98:10037-10041
71. Shrake A, Rupley JA. Environment and exposure to solvent of protein atoms-lysozyme and insulin. J Mol Biol. 1973;79:351-371
72. Sitkoff D, Sharp KA, Honig B. Accurate calculation of hydration free energies using macroscopic solvent models. J Phys Chem. 1994;97:1978-1988
73. Duan L, Liu X, Zhang JZ. Interaction entropy: A new paradigm for highly efficient and reliable computation of protein-ligand binding free energy. J Am Chem Soc. 2016;138:5722-5728
74. Laskowski RA, Swindells MB. LigPlot+: multiple ligand-protein interaction diagrams for drug discovery. J Chem Inf Model. 2011;51:2778-2786
75. Do P-C, Lee EH, Le L. Steered molecular dynamics simulation in rational drug design. J Chem Inf Model. 2018;58:1473-1482
Author contact
![]() Corresponding author: E-mail: hung.nvorg.vn (H.N).
Corresponding author: E-mail: hung.nvorg.vn (H.N).

 Global reach, higher impact
Global reach, higher impact